XY Wing (alias Y Wing)
XY Wing (soms ook Y Wing genoemd) is nog een extra geavanceerde oplosmethode voor het schrappen van kandidaten.
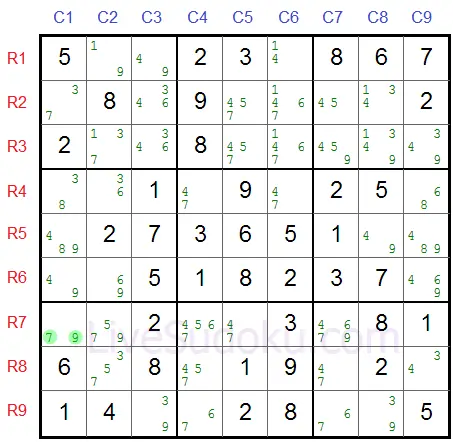
Alles begint met het vinden van een vakje met enkel twee kandidaten (een bi-waarde vakje) worde de pivot genoemd.
Deze 2 kandidaten noemt men X en Y.
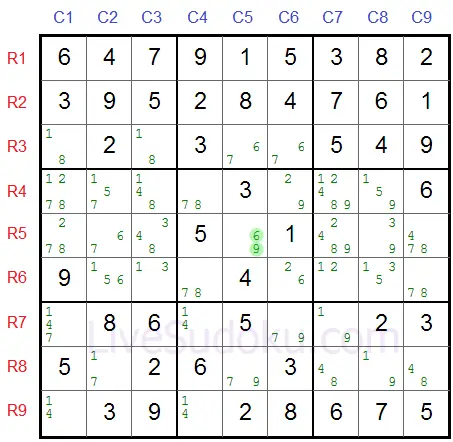
In ons voorbeeld - R5C5 is de pivot met X=6 en Y=9.
Hierop volgend gaan we op zoek naar twee andere vakjes met bi-waarden dat tegelijkertijd ook buddy vakjes zijn met de pivot.
Deze noemen we de nijptang, één vakje moet de X en Z bevatten als kandidaten en de andere - Y en Z.
Hierbij is Z een andere getal dan X en Y.
In ons voorbeeld is Z=7 en de zogenaamde nijptang bestaat uit R5C2 (zelfde rij als de pivot) en R8C5 (zelfde kolom).
Kandidaten voor R5C2 zijn 6 en 7 (X=6, Z=7).
Kandidaten voor R8C5 zijn 9 en 7 (Y=9, Z=7).
Binnen de XY Wing zijn we vooral geïnteresseerd in de Z-waarde en de andere vakjes waar deze invloed op hebben.
Er zijn maar twee mogelijke opties voor de pivot (6 of 9) en de nijptang om deze op te lossen:
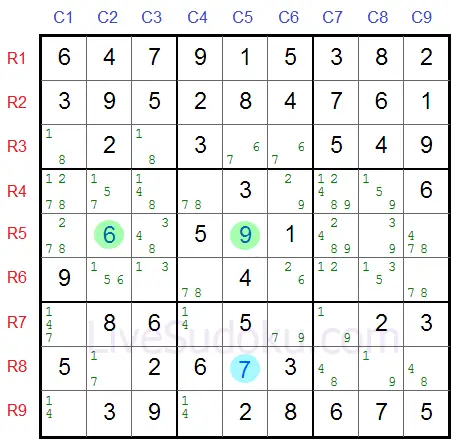
als pivot=6 (X) dan:
R8C5=9 (Y) en R5C2=7 (Z).
de andere mogelijkheid is, dat pivot=9 (Y) dan:
R8C5=6 (X) en R5C2=7 (Z).
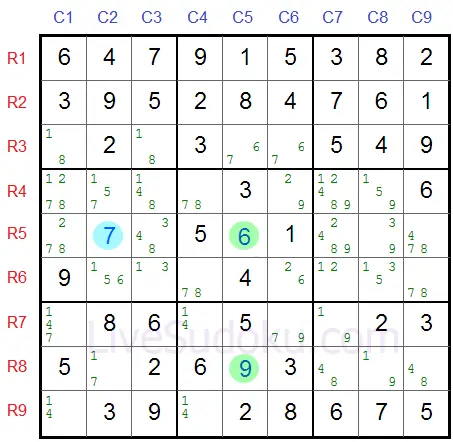
In eender welke manier zal de nijptang R5C2 of R8C5 gelijk aan 7 (Z) zijn, deze staan uitgelicht in blauw:
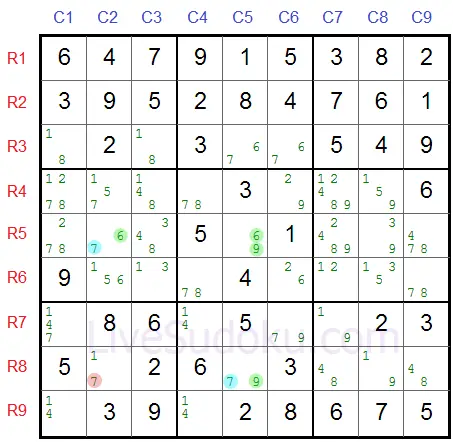
We kunnen dan ook concluderen dat elke vakje dat een buddy is van beide delen van de nijptang zoals R5C2 en R8C5 geen 7 (Z) kan bevatten.
Neem bijvoorbeeld R8C2 - we kunnen nu al getal 7 (Z) schrappen als kandidaat:
Het vorige voorbeeld had de vorm van een X maar dit is geen vereiste.
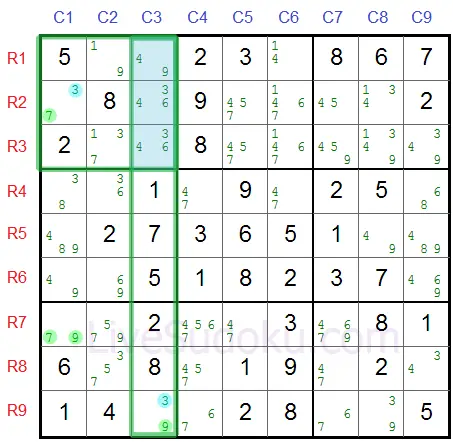
Om dit aan te tonen bekijken we het volgende voorbeeld waar R7C1 de pivot is:
R2C1 vormt het eerste deel van de nijptang (in dezelfde kolom als de pivot).
R9C3 is het overige deel van de nijptang (deze staat in hetzelfde vierkant als de pivot).
X=7, Y=9 en Z=3 (in blauw aangeduid)
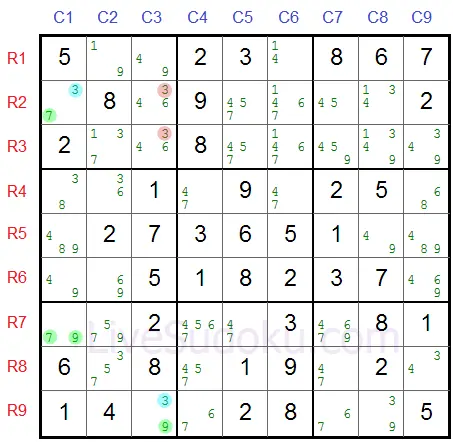
Elke vakje dat een buddy vormt met de beide delen van de nijptang R2C1 en R9C3 zal niet het cijfer 3 (Z) bevatten.
Dus alle vergelijkbare vakjes die een 3 bevatten als kandidaat, daar kunnen we deze 3 dan ook schrappen.
De buddy vakjes van beide delen van de nijptang staan in het blauw aangeduid.
Zie jij meteen in welke vakjes de 3 niet kan staan?
Het antwoord is zowel R2C3 als R3C3.
Deze vakjes staan in hetzelfde vierkant als het eerste deel van de nijptang - R2C1 en in dezelfde kolom als het tweede deel van de nijptang R9C3.
Deze vakjes kunnen geen 3 zijn dus we kunnen ze dan ook verwijderen van de lijst met kandidaten.
Deze keer hebben we de Z-waarde geschrapt van twee vakjes, XY is niet gelimiteerd invloed te hebben op slechts één vakje maar elk vakje waar deze regels toepasbaar op zijn.
Hoe deze gemakkelijk te herkennen
XY wings moeten 3 buddy vakjes hebben dat een bi-waarde (slechts 2 kandidaten elk) bezitten, dus het eenvoudigste om mee te beginnen is op zoek gaan naar 3 buddies met elk bi-waarden.
Deze 3 vakjes zullen XY, XZ en YZ kandidaten bevatten.
Eenmaal je dit scenario herkent, kan je op zoek gaan naar de buddy vakjes van zowel XZ en YZ en uiteindelijk de Z schrappen van de bovenstaande oplosmethode.